Time for another electric vehicle (EV) total cost of ownership (TCO) update for my 2014 Nissan Leaf SL. This is the eighth in a series – the earlier posts can be found at the “Cost Info Posts” page. I’ve now crossed 136,000 km (~85,000 miles) at the time of writing at just over the 3.5 year mark. Note that these costs are all $CDN.
I’ve also included a few bits of news I found of interest from the EV world in the last 6 months down below the cost information.
Cost Details
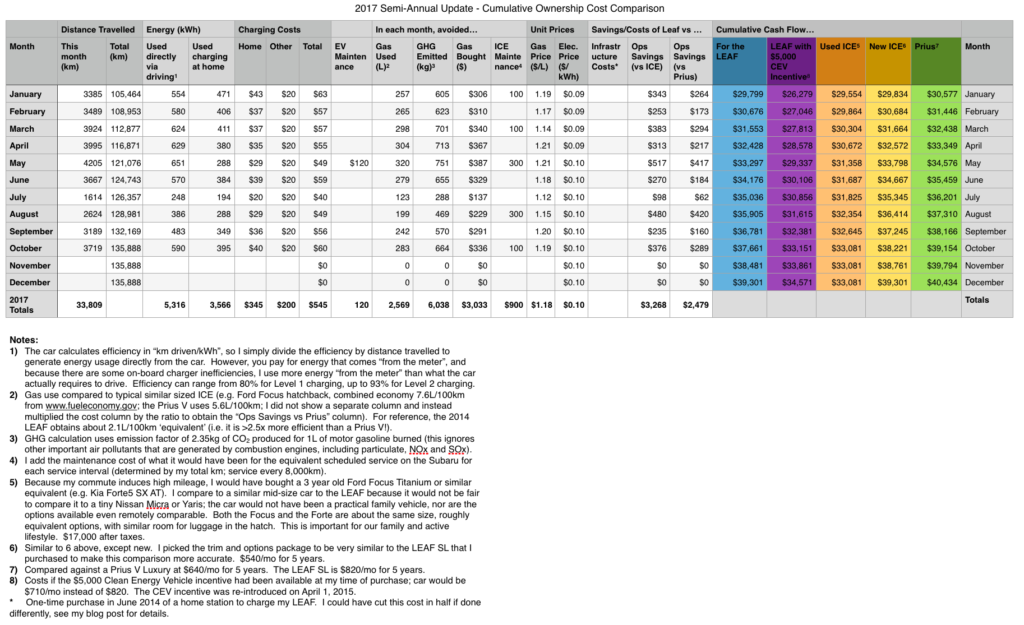
Read the first post in this series for an explanation on the comparisons I’ve made in the table below:
The total cost continues to be in the favour of the LEAF. As noted in the 3 year post, the EV stretched out its lead a bit further in this 6 month period because of additional maintenance that was scheduled for the gas car (which included some of the following: lubricant diagnosis, service mass air flow sensor, service throttle body). Cost of maintenance on the LEAF so far is $240!
The graph below shows the costs to date visually, and includes the forecast out to 8 years:

Actual costs at 3.5 years and 135,888 km, plus forecasted costs to 8 years – click to open larger version
When first creating this post series back in 2014, I figured that you would be able to reasonably purchase a used 2nd generation EV in the first half of 2018. The forecast shown above assumes I was able to sell my initial used internal combustion engine (ICE) car for $5,000 at 7 years old and roughly 225,000 km (140,000 miles) and purchase a used 2nd gen EV for ~ $30,000. So far that won’t be possible, since the only 2nd gen EV to-date is the Chevrolet Bolt, and as of today, there was only one used one listed in Canada for $40,000. During the next cost update, I’ll see if a used 2nd gen EV is even available…. though the used ICE would be likely to get VERY expensive with major repairs (transmission, possibly engine, etc) to carry on much past that many km’s.
I’m still forecasting the battery replacement about this time in 2018, after 4.5 years. At the end of August, I lost the first bar of capacity on my LEAF, which means my battery has about 85% of the original capacity available left for usage. On a daily basis, this hasn’t really affected me yet, as I charge fully at both end of my commute on a Level 2 charger. I was able to make it through two winters using a Level 1 charger at work, but now it wouldn’t be possible some days (since I arrive with around 25-30% in winter now, vs 30-35%: car can recharge 45% on Level 1 during the workday, and I need 75% now to have a safe cushion to get home).
But despite forecasting replacement in 2018, we’re not sure whether we’ll replace the battery next fall (I expect to be at about 80% capacity then), or if I’ll squeeze out another winter or two then replace it, or if instead we’ll replace the Forester with a similar SUV EV in 2019 or 2020 and relegate the LEAF to town driving only.
Addendum – Interesting news and tidbits in the past 6 months:
Sales of EVs in Canada are up 50% this year over 2016, and we have also broken the barrier of 1% of all vehicles sold as EVs! In a few years, we will see this % rise dramatically as we hit the upward part of the “S” curve of new technology adoption. Act now and you too can be classified as an “Innovator” 😉
Nissan released the next generation of the Nissan Leaf, which should hit the roads in Canada in early 2018. It will have a range of approximately 240 km. Sales have been very brisk in its home market of Japan, with ~3,600 sales in October!
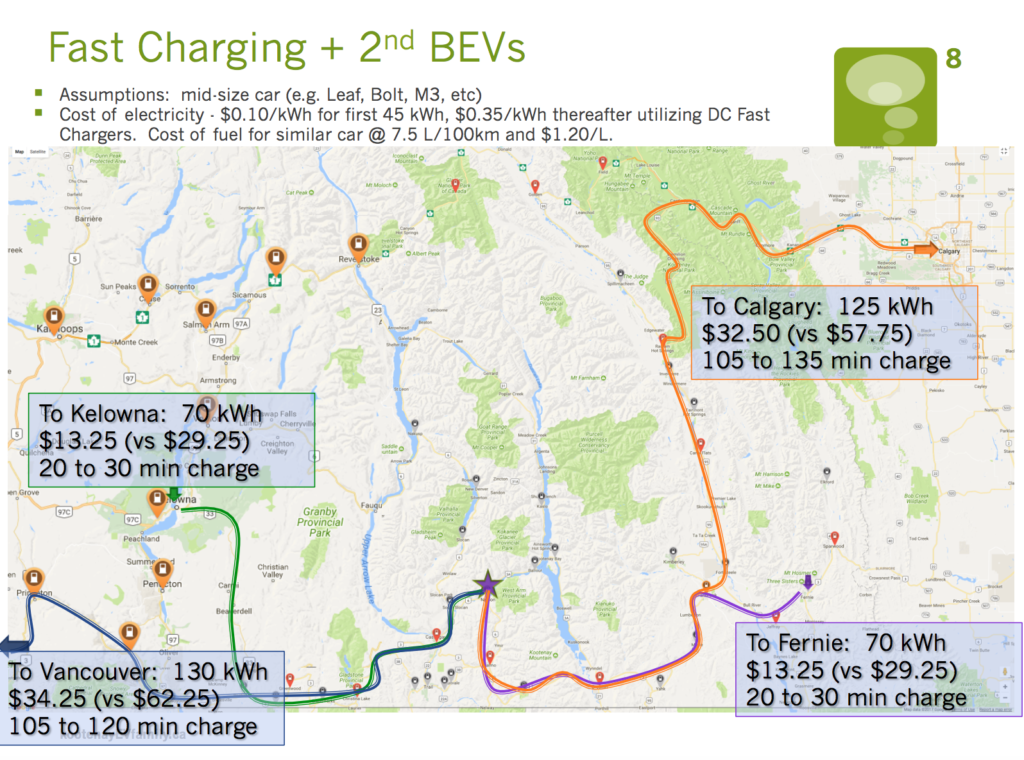
In October I attended the Green Home and Energy Show for the fourth year running, and also gave a presentation – this year I focused on 2nd gen EVs and fast charging networks and what it means for the Kootenays as the Accelerate Kootenays project ramps up – an excerpt is below. I plan to put together a more comprehensive post on the topic sometime this winter.
On November 16th, Tesla unveiled an important future product, the Tesla Semi. Watch the full reveal on YouTube here (unfortunately the video uploader cut out the awesome accompaniment music, probably some sort of copyright issue – Beastie Boys – Sabotage – my armchair guess is that the “thorn in [their] side” is the short-sellers and that the Semi [plus the other surprise reveal!] is their answer to that!) By the way, I watched the reveal live with a friend while drinking a beer… we were joking with each other about the fact that we were watching a semi-truck event and enjoying it! (Of course the surprise reveal at the end brought it to the next level.) There has been a raft of different analysis on the Semi already – my favourite is this one from a fleet company owner, and here is a different piece with a few questions from a trucker. The Semi isn’t the be-all end-all solution, but as you can see here, commercial transport (largely diesel vehicles, with environmentally harmful and carcinogenic emissions) is 23% of the GHG emissions in BC, more than the 14% of personal vehicles, so products like the Tesla Semi are hugely important.
- R1T Efficiency Tests: Bikes and Ski Boxes - March 30, 2024
- Adding Outdoor Accessories to my R1T - December 1, 2023
- Why an EV truck? Why the R1T? - October 8, 2023

Hi Andrew,
I have been interested in EV’s now for a couple of years, but since the infrastructure of chargers are so limited; I been holding off. I live in Golden BC actually 23km south of Golden and have 44km (one way) commute to work; I am the Head groomer of the Golden Nordic Ski Club:) Recently their was an announcement that Golden will get a Fast Charger this summer 2018; also the reason I found you. Now I am getting exited of maybe owning an EV.
How much would a replacement battery cost for your 2014 Nissan Leaf?
If you would sell your Leaf,do you think its battery be good enough for my commute, and for how many more years?
Your posts are fantastic, thanks for all your hard work and efforts to make EV’s a reality in our part of BC.
Erwin, I just noticed this comment, sorry I didn’t answer sooner! With the elevation that you have to climb and the colder weather you experience in Golden as compared to Nelson, I don’t think you would be able to do that round-trip in a 24 kWh Leaf. You should be able to that trip in a 30 kWh car though (2016 SV/SL, any 2017), probably until the car is about 4-5 years old. At that point you might need a 5 minute top-up at the DCFC.
We aren’t entirely sure what replacement cost in Canada will be yet – in the US they were advertised at $5500, which I translated to be about $7500 in Canada. I haven’t checked into it yet, because I am still holding off.
Thank you for your response Andrew. That was my plan, to top up at the DCFC, before going up to the Nordic Center. By the way do you know when this installation (DCFC) will be happen in Golden? Also thanks for suggesting looking into a newer vehicle with a 30kWh pack. I might have to wait though for a couple of years before prices come down, as you have noted in your latest update.
Thank you for your post and making EV a reality in the Kootenay’s and Columbia’s. Erwin
Ah, well if you are fine using the DCFC, then you should be able to top-up on your way home at the end of the day. Or you could maybe plug in during the day? Even a 110V outlet should get you enough juice. There are some pretty good deals out there on 2013 and newer Leafs. I would get an SV so you have the heat pump, the 6.6 kW charger, and fast charge (DCFC) port.
As to when the DCFC will be installed, I don’t know the answer to that for sure, but my understanding was that they would all be installed by the end of 2018. You could try emailing the folks at Accelerate Kootenays to see if they can give more specific information.